最近在重构需求的时候，使用到了DAG. 隐隐约约觉得之前接触过。因为在学校里老师在讲数据结构的时候讲过“图”，因此我坚信之前肯定学过，只不过是忘了而已。幸好这次有一个可以使用它解决实际问题的机会，所以写个文章记录一下它的原理。
最近在重构需求的时候，使用到了DAG. 隐隐约约觉得之前接触过。因为在学校里老师在讲数据结构的时候讲过“图”，因此我坚信之前肯定学过，只不过是忘了而已。幸好这次有一个可以使用它解决实际问题的机会，所以写个文章记录一下它的原理。
DAG定义
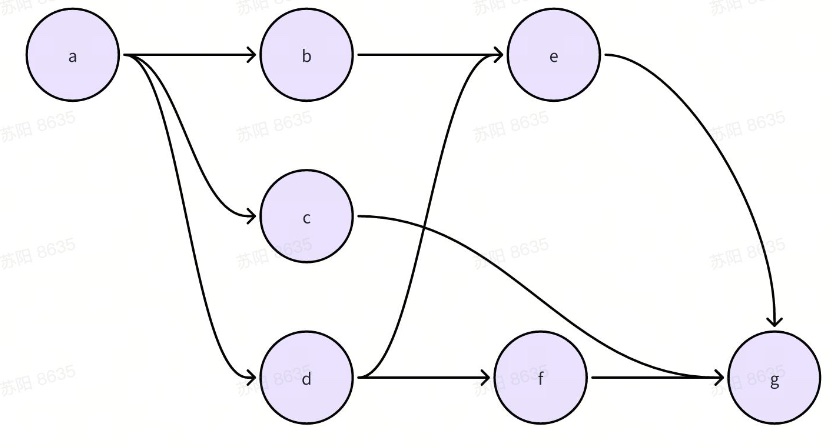
在图论中，如果一个有向图从任意顶点出发无法经过若干条边回到该点，则这个图是一个有向无环图（Directed Acyclic Graph）。比如下图就是一个典型的DAG
拓扑排序
节点入度：有几条边指向改节点，上图中e节点的入度是2 节点出度：从该节点出发有几条边，上图中e节点的出度是1
拓扑排序（Topological Sorting）是一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列。且该序列必须满足下面两个条件：
- 每个顶点有且仅出现一次。
- 若存在一条从顶点 a 到顶点 b 的路径，那么在序列中顶点 a 出现在顶点 b 的前面。
排序的算法也比较简单
- 找到入度为0的节点，并他们加入序列
- 将与1中相连接的节点的入度减1
- 重复1、2步，知道所有的节点都已排好序
值得强调的是，拓扑排序的结果不是唯一的，还是拿上图举例，它的拓扑排序的结果可以是 [a, b, c, d, e, f, g] 也可以是 [a, c, b, d, e, f, g] 因为当a节点被纳入序列后，b、c、d三个节点的入度都是0，因此他们谁先加入序列都是可以的
执行流程
大致的流程是
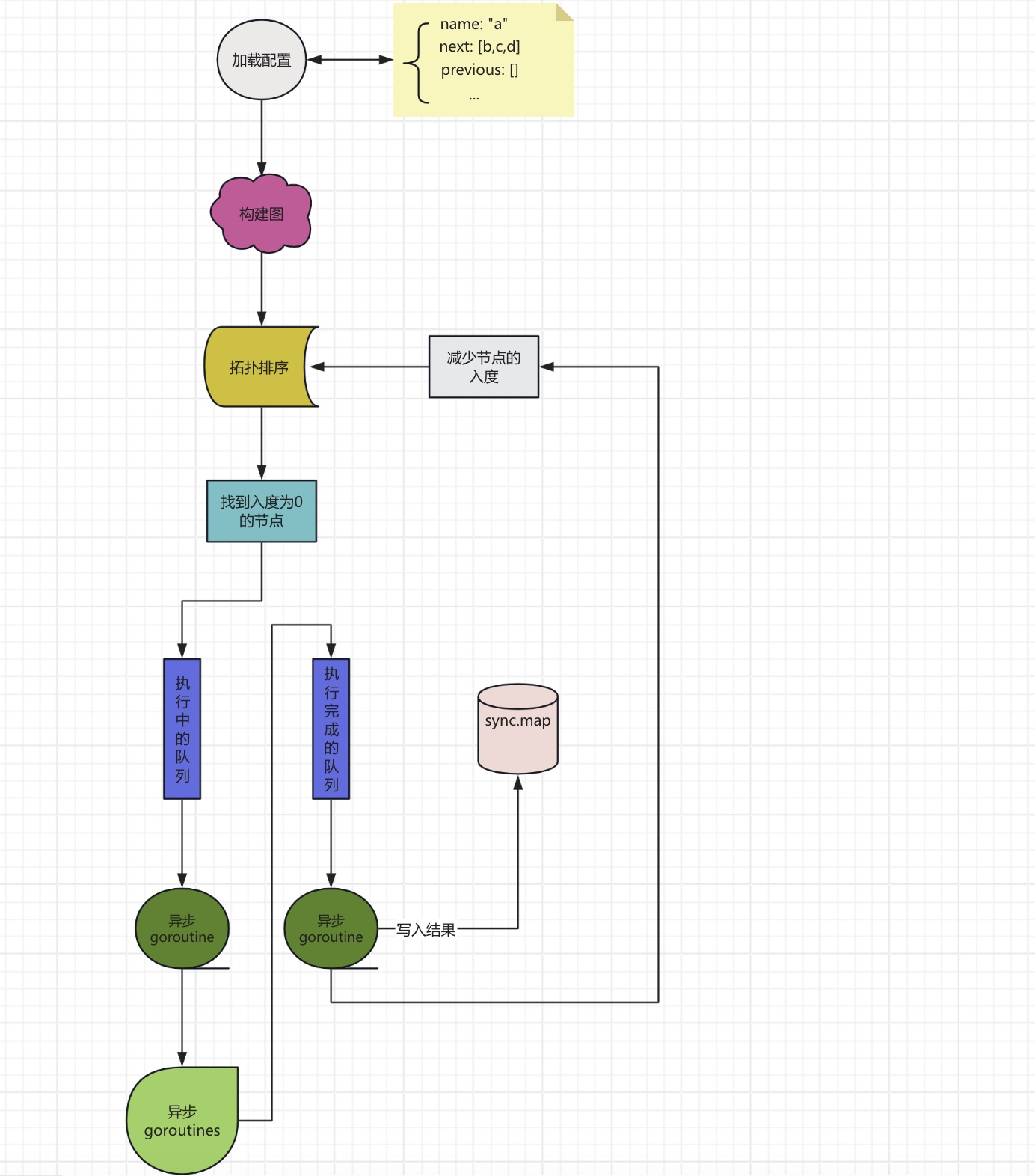下面再用文字对整体流程做个补充
- 每一个DAG都会有一个json配置，其中比较重要的信息就是描述了各个节点之前的节点有哪些，之后的节点有哪些
- 在主协程中依次加载配置、根据依赖关系构建图、拓扑排序，在这个过程会检查图有没有环
- 初始化两个chan，一个用于保存目前可以执行的节点，另一个用于保存执行完的节点
- 初始化两个异步的协程，分别监听步骤4中的2个chan，但是他们的模式是不相同的。监听已完成chan的协程不会开启异步协程去处理，而是自己完成所有的逻辑
- 寻找入度为0的节点加入可以执行的chan。监听可以执行的chan的协程一旦获取到了数据会再次开启一个异步的协程去执行，这也是节点之间可以并发执行的原因。
- 节点执行完以后会将其放入执行完成的队列，监听该队列的协程会将结果写入sync.map中，同时会将该节点的next节点的入度减一
- 重复执行6，直到所有的节点都执行完成